3 Shocking Ways to Break Mathematics

This post provides formal proofs of three paradoxes that occur in type systems with unrestricted recursion, negative data types, or type in type (Girard’s paradox). The title is a pun on BuzzFeedy headlines. The source code of the paradoxes is available for download.

An important aspect of type theory is identifying the values of a given type. For example: the values of type $\mathbb{N}$ are the natural numbers $0, 1, 2, \dots$; the values of type $\text{bool}$ are $\text{true}$ and $\text{false}$. This blog post explains ways in which many languages add spurious values to types. In Java, for example, there are at least 3 values of type boolean¹.

A type system that avoids spurious values has several advantages. For example:

1) A type system can provide guarantees about a program. For example, a type system can guarantee that the function $\text{square}(n : \mathbb{N}) := n^2$ is only ever invoked with a natural number (not e.g. a string) and thus that $n^2$ will never fail. Spurious values can break these guarantees.

2) A type system can enable mathematical reasoning using the Curry-Howard Correspondence. Using this correspondence, true propositions are represented by inhabited types (i.e. at least one value is of the type), and false propositions are represented by uninhabited types (i.e. no value is of the type). A spurious value in a type intended to be uninhabited (e.g. False), leads to a true proposition that was intended to be false — a paradox.

The examples of spurious values in this blog post are based on divergence, and are thus mostly interesting for mathematical reasoning (the second advantage).

Unrestricted Recursion

Most programming languages allow some form of unrestricted recursion or loops, which can usually be exploited to construct a value of an arbitrary type. For example, the Java expression f() (defined below) is of type boolean but neither true nor false.

public static boolean f() {
  return f();
}

The trick is that f never actually has to generate a boolean value, because it delegates that responsibility to itself by calling f. By delegating all the work to itself though, f never gets anything done.

Every typed mainstream programming language has this problem (including Haskell and ML). While this seems bad, it’s not quite as bad as you might expect initially. In Java, a function g that takes a boolean is still guaranteed to only ever be invoked with a value that is either true or false (unless Java is broken in some other way). The reason is that g(f()) never actually calls the function g, because f never stops executing.

If you want to use Java’s type system for mathematical reasoning though, you will be pleased to hear (sarcasm) that every single proposition will be true, because there is a value in every type.

Languages can avoid these kinds of spurious values/paradoxes, for example by using inductive data types and eliminators instead of unrestricted recursion.

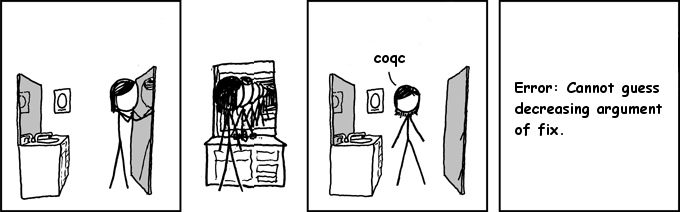
Negative Data Types

Functional programming languages like Haskell and ML provide algebraic/inductive data types. These can be exploited to construct a value of an arbitrary type. For example, the expression false below inhabits the inductive type False which was defined to have no constructors.

data False

data Rec a = Rec { rec :: Rec a -> a }

false :: False
false = rec (Rec (\a -> rec a a))
            (Rec (\a -> rec a a))

Note that false diverges because it reduces to (\a -> rec a a) (Rec (\a -> rec a a)) which reduces back to false. This program is inspired by Adam Chlipala’s book CPDT, chapter 3.6.

Languages can avoid these kinds of spurious values/paradoxes by restricting the shape of an inductive type T. Specifically, the type of a constructor of T may not refer to T on the left side of a function arrow. This restriction is called strict positivity.

Type in Type

Most typed languages allow functions that take terms as arguments, for example not (b:bool) := if b then false else true. More advanced type system also allow functions that take types are arguments, for example id (A:Type) (a:A) := a. In such languages, the question arises what the type of Type should be. Initial suggestions were for Type to be of type Type, i.e. Type : Type, until Girard proved that this is paradoxical. The following proof is based on Per Martin-Löf’s proof of Girard’s paradox in An Intuitionistic Theory of Types, 1972.

Note that this problem only arises in languages with fairly complex type systems. Many languages simply do not allow a programmer to ask for the type of Type. In Java for example, the function static <A> A id(A a) { return a; } takes the type A as argument, but because there is the special syntax <A> Java gets away without having to type the expression Type.

This proof will define a notion of ordering, will show that orderings can themselves be ordered, will show that all orderings are smaller than the ordering of orderings, and will conclude that this is a contradiction. Don’t despair if all this talk of orderings of orderings makes your head hurt. This is the expected behavior — your brain has evolved to avoid wasting resources on thinking diverging thoughts.

This paradox relies heavily on the notion of an ordering, which requires that we first become familiar with transitivity and infinite chains.

Definition transitive {A:Type} R := forall (x y z:A), R x y -> R y z -> R x z.

Definition infiniteChain {A:Type} R (f:nat->A) := forall n, R (f (S n)) (f n).

Given a binary relation over A, a function f is called an infinite chain if it assigns to each natural number n a value f n in A, such that the value assigned to the next number f (S n) is related to f n.

For example, the identity function id is an infinite ascending chain of the natural numbers.

Lemma infiniteAscendingChainNat : infiniteChain gt id.
  unfold infiniteChain, id.
  intro n.
  omega.
Qed.

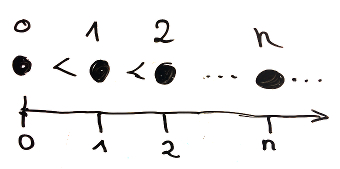
Yet, it is impossible to create an infinite descending chain of the natural numbers. Consider for example the failed attempt of assigning some number m to f 0 and then subtracting n from m at f n. This fails because for n >= m the subtraction m - n is defined to be 0. Note that there exist infinite descending chains for the integers and real numbers.

Lemma infiniteDescendingChainNat m : infiniteChain lt (fun n => m - n) -> False.
  unfold infiniteChain.
  intro h.
  specialize (h m).
  omega.
Qed.

We define an ordering as a set together with a “less than” relation that is transitive and contains no infinite descending chains (note that the ordering is not required to be total). Note that ordering could be defined using existentials instead of a record.

Class ordering : Type := {
  set : Type;
  lt : set -> set -> Type;
  trans : transitive lt;
  noChains : forall f, infiniteChain lt f -> False
}.
Notation "x < y" := (lt x y).

Such an ordering is necessarily irreflexive.

Lemma irreflexive `{ordering} a : a < a -> False.
  intro h.
  apply (noChains (fun _ => a) (fun _ => h)).
Qed. 

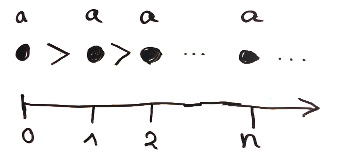
All the paradoxes we have seen so far are based on recursion. It should come to nobody’s surprise that this paradox will go the same way. Therefore, we now define the ordering of orderings.

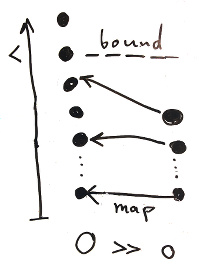
An ordering o is less than an ordering O, if and only if there exists an order preserving map that takes every element in o’s set to an element in O’s set, and there exists a bound in O’s set that is larger than the mapping of every element in o’s set.

Class orderingLe (o:ordering) (O:ordering) : Type := {
  map : @set o -> @set O; 
  mapOk x y : x < y -> map x < map y; 
  bound : @set O;
  boundOk x : map x < bound
}.
Notation "x << y" := (orderingLe x y) (at level 45).

Pictorially, we will represent two ordered orderings o and O as:

To show that << is an ordering, we have to show that << is transitive.

Lemma orderingLeTransitive : transitive orderingLe.
  compute.
  intros o o' o'' ? ?.
  refine {|
    map := map ∘ map; 
    bound := bound 
  |}.
  + intros.
    apply mapOk.
    apply mapOk.
    trivial.
  + intro x.
    apply boundOk.
Qed.

The new map of the ordering is the functional composition of the other orderings’ maps, the new bound is the larger ordering’s bound. This new map is clearly order preserving, and the new bound a bound.

Pictorially:

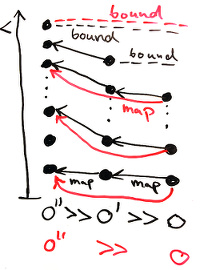
Further, we also have to show that << contains no infinite descending chains. To this end, it is sufficient to show that an infinite descending chain f of orderings implies the existence of an infinite descending chain g in the ordering f 0 (which is a contradiction).

Definition chainImpliesChain f : infiniteChain orderingLe f -> {g:nat -> set & infiniteChain (@lt (f 0)) g}.
  intro h.
  unfold infiniteChain in *.
  refine (
    let fix rec n' := 
      match n' as n'' return @set (f n'') -> @set (f 0) with 
      | 0 => id
      | S n'' => rec n'' ∘ map
      end in _).
  refine (existT _ _ _).
  + exact (fun n => rec n (@bound _ _ (h n))).
  + cbn.
    intro n.
    enough (forall x y, x < y -> rec n x < rec n y) as h'. {
      apply h'.
      apply boundOk.
    }
    intros x y.
    induction n as [|n IHn]; cbn in *.
    * trivial.
    * intro h'. 
      apply IHn.
      apply mapOk.
      apply h'.
Qed.

Lemma orderingLeNoChains f : infiniteChain orderingLe f -> False.
  intro h.
  destruct (chainImpliesChain f h) as [g h'].
  refine (@noChains (f 0) g h').
Qed.  

The infinite descending chain g assigns to n the bound of the ordering f n mapped to an element in the set of the ordering f 0. i.e. g 0 := bound, g 1 := map bound, g 2 := map (map bound), g 3 := map (map (map bound)), etc. g is an infinite descending chain because the maps are order preserving, and the objects in f (S n) are bounded by the bound of f n.

This can be represented pictorially. Note that the y-axis’s < is flipped, i.e. objects on the bottom are larger than objects on the top.

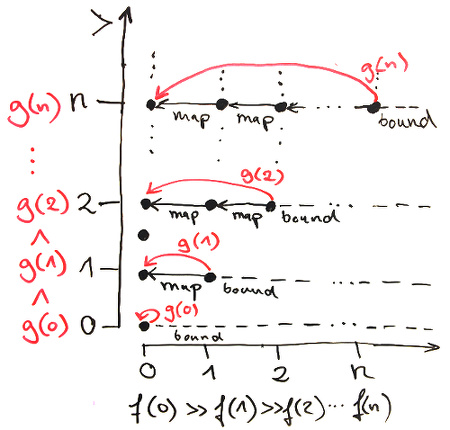
We are now ready to define the ordering of orderings. To avoid paradoxes exactly like the one we are currently defining, Coq does not allow this definition. Thankfully, the flag -type-in-type makes Coq more lenient.

Instance orderingOfOrderings : ordering.
  refine {| set := ordering; lt := orderingLe |}.
  + apply orderingLeTransitive.
  + apply orderingLeNoChains.
Defined.

We will need the notion of a sub-ordering of the ordering o. A sub-ordering is defined to be a subset of o’s set containing all the elements of o smaller than a bound a. A sub-ordering has the same ordering relation a o, and is thus trivially transitive and contains no infinite descending chains.

Instance subOrdering (o:ordering) (a:@set o): ordering.
  refine {| 
    set := {x:@set o & x < a}; 
    lt := fun x y => projT1 x < projT1 y
  |}.
  + intros [x ?] [y ?] [z ?].
    cbn.
    apply trans.
  + intros f h.
    apply (noChains (fun n => projT1 (f n))).
    intro n.
    specialize (h n).
    apply h.
Defined.

A sub-ordering is always smaller than the original ordering, and a sub-ordering with a smaller bound a is smaller than a sub-ordering with a larger bound b.

Lemma subOrderingIsLt {o:ordering} : forall a, subOrdering o a << o.
  intro a.
  cbn.
  refine {| 
    map := _;
    bound := a
  |}.
  * exact (fun x => projT1 x).
  * intros [x ?] [y ?].
    cbn.
    exact (fun a => a).
  * intros [x h].
    cbn.
    apply h.
Qed.

Lemma subOrderingOrderPreserving {o:ordering} a b : a < b -> subOrdering o a << subOrdering o b.
  intros h.
  refine {|
    map := _;
    mapOk := _;
    bound := _;
    boundOk := _
  |}.
  * refine (fun x => existT _ (projT1 x) _).
    specialize (projT2 x); intro h'.
    specialize trans.
    firstorder.
  * intros [] [].
    cbn in *.
    trivial.
  * refine (existT _ a _).
    trivial.
  * cbn in *.
    intros [].
    cbn.
    trivial.
Qed.

The next step is to show that the ordering of orderings is larger than all orderings o. This is done by mapping all elements of o into a sub-ordering.

Lemma orderingOfOrderingsBound o : o < orderingOfOrderings.
  cbn.
  refine {| 
    map := fun a => subOrdering o a;
    bound := o
  |}.
  + apply subOrderingOrderPreserving.
  + apply subOrderingIsLt.
Qed.

Pictorially:

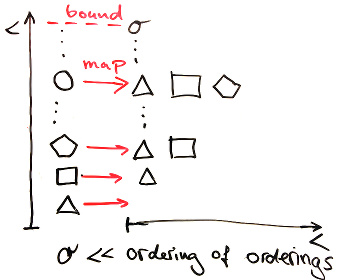
We just showed that the order of orderings is larger than all orderings (including itself), and we also showed that orderings are irreflexivity. This is clearly a paradox.

Lemma orderingOfOrderingsReflexive : orderingOfOrderings < orderingOfOrderings.
  apply orderingOfOrderingsBound.
Qed.

Theorem false : False.
  apply (@irreflexive orderingOfOrderings orderingOfOrderings).
  apply orderingOfOrderingsReflexive.
Qed.

The paradox is caused by the self-referential nature of the ordering of orderings. In general, the definition of a type is called impredicative if it involves a quantifier whose domain includes the type currently being defined (see TaPL, chapter 23). A predicative type system enforces that such self-referential definitions cannot be made. Predicative type system are usually implemented using stratification or ramification, where Type is indexed by a natural number and Type n : Type (n + 1), e.g. Type 0 : Type 1 : Type 2.

Stratification is also the trick that Haskell uses to avoid this paradox (it’s not like that matters, given that the other two paradoxes are still possible). Instead of having an infinite hierarchy of types though, Haskell opts for just a finite number of them (the highest being kinds).

Conclusion

The types of most languages contain spurious values and are thus not useful for mathematical reasoning using the Curry-Howard Correspondence. Languages free of all known paradoxes are for example Coq, Agda, NuPRL, and Lean.

Footnotes